Когда речь идет об измерении и представлении данных, точность имеет решающее значение. В науке, технике или других дисциплинах важно понимать понятия абсолютной и относительной погрешности. Эти две меры помогают количественно выразить разницу между измеренными и фактическими значениями, предоставляя ценную информацию и обеспечивая достоверность результатов.
Абсолютная погрешность - это разница между измеренным и истинным значением величины. Она представляет собой численное выражение того, насколько далеко измеренное значение от точного или идеального. Абсолютная погрешность обычно выражается положительным числом, так как учитывается только величина разности.
Например, измеряется длина стола, и фактическое значение равно 100 см. Если измеренное значение равно 95 см, то абсолютная погрешность составляет 5 см.
Относительная погрешность, напротив, учитывает и размер, и масштаб измеряемой величины. Она выражается в виде коэффициента, сравнивающего абсолютную погрешность с истинным значением. Эта мера позволяет определить точность измерения по отношению к величине измеряемой величины.
Продолжая предыдущий пример, если абсолютная погрешность составляет 5 см, а истинное значение - 100 см, то относительная погрешность равна 5% (5/100 * 100%). Это означает, что измеренное значение на 5% меньше действительного.
Понимание абсолютной и относительной погрешности важно в различных областях, таких как физика, химия и статистика. Они не только помогают оценить точность измерения, но и дают возможность сравнить надежность различных измерений и экспериментальных установок. Понимание и применение этих понятий позволяет уменьшить погрешность измерений, повысить точность и обеспечить достоверность результатов.
Что такое абсолютная погрешность?
Абсолютная погрешность - это широко используемое понятие при оценке точности измерений или вычислений. Абсолютная погрешность количественно определяет разницу между измеренным или рассчитанным значением и фактическим или ожидаемым значением. Это мера того, насколько далеко измерение или вычисление отстоит от истинного значения.
Абсолютная погрешность выражает величину разности между значениями и поэтому обычно выражается положительной величиной. Она может использоваться для оценки точности и достоверности измерений или расчетов.
Расчет абсолютной погрешности предполагает нахождение фактической разницы между измеренной или рассчитанной ценой и фактическим или ожидаемым значением. Это можно сделать, отняв фактическое значение от измеренного или рассчитанного. Полученная абсолютная погрешность может быть использована для оценки точности измерения или расчета.
Абсолютная погрешность часто выражается в процентах, так называемая относительная абсолютная погрешность. Это облегчает сравнение и интерпретацию точности различных измерений или расчетов. Относительная абсолютная погрешность рассчитывается путем деления конечной погрешности на действительное или ожидаемое значение, которое затем переводится в проценты путем умножения на 100.
Определения и расчеты
Абсолютная и относительная погрешности - это показатели разницы между расчетной или предполагаемой ценой и фактическим или точным значением. Эти показатели широко используются в различных областях, включая математику, физику и инженерное дело.
Итоговая погрешность - это величина разницы между расчетной и фактической ценами. Она представляет собой фактический размер ошибки. Абсолютная погрешность всегда выражается положительной величиной, поскольку она измеряет расстояние между двумя величинами независимо от направления. Человек абсолютной ошибки выглядит следующим образом.
Абсолютная погрешность = | истинное значение - расчетная цена|
Сопутствующая ошибка - это причина абсолютной погрешности по отношению к истинному значению. Учет величины ошибки, связанной с действительным значением, обеспечивает более стандартизированную меру погрешности. Сопутствующая погрешность выражается в процентах или десятичных числах. Соответствующие виды погрешности имеют следующие значения.
Погрешность = (абсолютная погрешность / истинное значение) x 100%.
Расчет абсолютной и сопутствующей погрешности позволяет лучше понять точность и достоверность расчета или оценки. Эти измерения позволяют получить информацию о качестве и надежности математических моделей, экспериментальных данных или вычислительных алгоритмов. Количественно оценивая погрешности, ученые и инженеры могут оценить значимость отклонений от фактических значений и принимать документированные решения с учетом уровня погрешности.
Последствия в измерениях.
Понимание абсолютной и относительной погрешности крайне важно в области измерений в науке, технике и любой другой отрасли, где требуется получение точных данных. При проведении измерений неизбежно возникает некоторая погрешность. Знание того, как интерпретировать и вычислять эту погрешность, необходимо для обеспечения надежности и достоверности результатов.
Абсолютная погрешность - это разница между измеренным значением и истинным или известным значением, которая дает представление о точности измерения. Она помогает выявить систематические ошибки в процессе измерения и позволяет при необходимости внести коррективы. Количественная оценка абсолютной погрешности позволяет ученым и инженерам лучше понять ограничения и неопределенности измерений.
Относительная погрешность, с другой стороны, представляет собой отношение абсолютной погрешности к истинному значению. Она выражает величину погрешности относительно истинного значения в процентах или долях. Эта метрика особенно полезна при сравнении различных показателей или оценке производительности различного оборудования или методов сбора данных. Учитывая относительную погрешность, можно определить наиболее точный и прецизионный метод измерения.
Кроме того, понимание абсолютной и относительной погрешности может помочь в процессе принятия решений. Оно позволяет оценить качество измерений и определить, насколько результаты приемлемы для предполагаемого применения. Например, в области медицины точные измерения необходимы для правильного введения лекарств и диагностики заболеваний. Учитывая абсолютные и относительные погрешности, медицинские работники могут обеспечить безопасность и эффективность лечения.
Таким образом, понимание абсолютной и относительной погрешности имеет решающее значение для измерений. Оно позволяет ученым, инженерам и специалистам различных профилей оценивать точность и надежность данных, вносить необходимые коррективы и улучшения, а также принимать обоснованные решения на основе результатов измерений. Без такого понимания надежность и достоверность измерений могут быть скомпрометированы, что приведет к неточным выводам и потенциально вредным результатам.
Пример.
Некоторые примеры, помогающие понять понятия абсолютной и относительной погрешности
- Пример 1: Предположим, что вы измеряете длину отрезка веревки, и фактическая длина составляет 10 см. Если измеряемая длина равна 9 см, то абсолютная погрешность составляет 10 - 9 = 1 см. Относительная погрешность составляет (1 / 10) * 100% = 10%.
- Пример 2: Необходимо вычислить площадь квадрата с длиной стороны 5 см. Фактическая площадь составляет 25 кв. см. Если вычисленная площадь равна 24 кв. см, то абсолютная погрешность составляет 25 - 24 = 1 кв. см. Относительная погрешность составляет (1 / 25) * 100% = 4%.
- Пример 3: Рассмотрим ситуацию, когда измеряется температура в помещении, а фактическая температура составляет 25 градусов Цельсия. Если результат измерения равен 24 градусам Цельсия, то абсолютная погрешность составляет 25 - 24 = 1 градус Цельсия. Относительная погрешность составляет (1 / 25) * 100% = 4%.
Что такое относительная погрешность?
Относительная погрешность - это понятие, используемое в математике и естественных науках для измерения точности вычислений или измерений; часто используется при сравнении двух величин для определения того, насколько они близки друг к другу. Относительная погрешность выражается в процентах или десятичных дробях и представляет собой разницу между вычисленным или измеренным значением и фактическим или ожидаемым значением.
Для расчета относительной погрешности сначала необходимо найти абсолютную погрешность. Это абсолютная разность между рассчитанным или измеренным значением и действительным или ожидаемым значением. Затем абсолютная погрешность делится на фактическое или ожидаемое значение, а полученный результат умножается на 100, чтобы получить относительную погрешность в процентах.
Относительная погрешность особенно полезна при сравнении измерений или вычислений с использованием различных единиц измерения или шкал. Она позволяет оценить точность значения без учета его абсолютной величины. Например, при сравнении высоты двух людей в метрах или футах относительная погрешность может быть использована для определения того, насколько близки друг к другу измеренные высоты.
Важно отметить, что относительная погрешность является относительной мерой точности и не указывает на правильность вычисленного или измеренного значения. Даже если относительная погрешность мала, это не обязательно означает, что значение является точным, так как оно может значительно отличаться от фактического или ожидаемого значения. Аналогично, большая относительная ошибка не обязательно означает, что значение неточное, так как оно может быть близко к фактическому или ожидаемому значению.
Определения и расчеты
Абсолютная погрешность - это мера того, насколько измеренная или рассчитанная величина далека от истинного или допустимого значения. Она представляет собой разность между измеренным и точным или известным значением. Абсолютная погрешность всегда положительна.
Для расчета абсолютной погрешности необходимо вычесть измеренное или рассчитанное значение из действительного или допустимого значения и получить абсолютное значение разности. Формула для расчета абсолютной погрешности имеет вид.
Абсолютная погрешность = | измеренное значение - истинное значение|
Относительная погрешность - это мера точности измеренного или рассчитанного значения по сравнению с величиной измеренного или рассчитанного значения. Она выражается в процентах или в виде десятичного числа. Относительная погрешность помогает сравнивать точность различных измерений или вычислений.
Для расчета относительной погрешности необходимо абсолютную погрешность разделить на действительное или допустимое значение и умножить на 100, чтобы перевести в проценты. Формула для расчета относительной погрешности выглядит следующим образом
Погрешность = (абсолютная погрешность / истинное значение) x 100
Абсолютная и относительная погрешности являются важными понятиями в научных и инженерных измерениях. Абсолютная погрешность дает информацию о величине погрешности, а относительная - о величине погрешности относительно величины измеряемой или вычисляемой величины.
Примечание: В некоторых случаях относительная погрешность рассчитывается путем деления абсолютной погрешности на измеренное или рассчитанное значение, а не на действительное или допустимое значение. Важно указать, какое значение используется при обозначении относительной погрешности.
Сравнение с абсолютной погрешностью
При изучении численного анализа абсолютная погрешность и относительная погрешность - две меры, обычно используемые для оценки точности вычислений и измерений. Абсолютная погрешность указывает на величину разности между приближенным и истинным значением, а относительная погрешность - на относительную меру этой разности.
Абсолютная погрешность определяется как разность между оцененным или рассчитанным значением и истинным или точным значением. Она показывает, насколько далеко приблизительное значение от истинного. Абсолютная погрешность обычно выражается в тех же единицах, что и истинное значение, что облегчает ее интерпретацию. Этот показатель полезен в тех случаях, когда имеется четкая точка отсчета или известное фактическое значение, с которым можно сравнивать.
Относительная погрешность, с другой стороны, измеряет точность аппроксимации в процентах или соотношении. Она рассчитывается путем деления абсолютной погрешности на истинное значение и умножения на 100. Относительная погрешность представляет собой относительную меру отклонения от точного значения и позволяет сравнивать различные величины разных размеров. Это может быть ценным показателем при работе с величинами, сильно различающимися по размеру.
При сравнении абсолютной и относительной погрешностей важно учитывать обстоятельства и цель измерения или вычисления. Абсолютная погрешность более уместна, когда речь идет о фактической разнице между приблизительными и истинными значениями, в то время как относительная погрешность более подходит для сравнения точности различных вычислений или измерений. Оба показателя имеют свои преимущества и ограничения и должны использоваться в соответствии с конкретной ситуацией.
Применение в реальном мире
Понимание абсолютной и относительной погрешности необходимо в различных реальных приложениях, особенно в тех областях, где измерения и вычисления играют важную роль. Вот некоторые примеры
- Проектирование и строительство: абсолютная и относительная погрешность помогает инженерам и архитекторам обеспечить точность при проектировании и строительстве. Будь то расчет точных размеров здания или определение допусков на механические детали, понимание этих понятий необходимо для того, чтобы избежать дорогостоящих ошибок.
- Наука и исследования: точные измерения имеют первостепенное значение при проведении научных экспериментов и исследований. Анализ абсолютных и относительных погрешностей используется для оценки и подтверждения результатов экспериментов и обеспечения достоверности выводов, сделанных на основе полученных данных. Кроме того, он помогает ученым оценить точность научных моделей и симуляторов.
- Финансы и экономика: финансовые институты в значительной степени зависят от точности расчетов процентных ставок, инвестиций и оценок активов. Понимание абсолютных и относительных ошибок позволяет экономистам и финансовым аналитикам оценивать точность и надежность финансовых моделей и прогнозов. Оно также может помочь в оценке рисков и принятии решений.
- Контроль качества и производство: обеспечение качества и согласованности продукции имеет решающее значение в производственном процессе. Анализ абсолютных и относительных погрешностей используется для измерения и контроля уровня отклонений между заданными техническими характеристиками и фактически измеренными значениями. Это помогает производителям выявлять и устранять отклонения, что приводит к повышению качества продукции и удовлетворенности клиентов.
- Медицина и фармацевтика: В медицине точные измерения и расчеты необходимы для диагностики пациентов, введения лекарств и проведения медицинских исследований. Анализ абсолютных и относительных погрешностей используется для определения точности и прецизионности диагностических тестов, оценки надежности медицинских приборов и эффективности фармацевтических препаратов.
Эти области применения являются лишь одним из примеров того, какое большое значение имеет понимание абсолютной и относительной погрешности в самых разных областях. Эффективное использование этих понятий позволяет специалистам минимизировать влияние ошибок и принимать обоснованные решения на основе точной и достоверной информации.

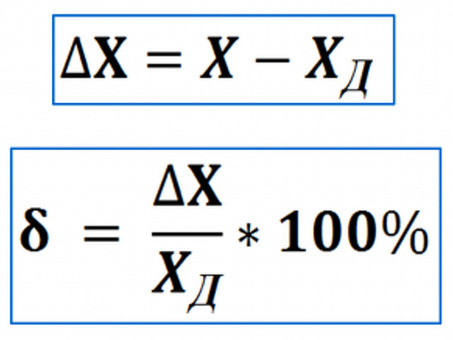


Комментарии