Значимость t-теста Стьюдента

t-тест Стьюдента, названный так по имени его создателя Уильяма Сили Госсета, представляет собой статистический тест, используемый для сравнения средних значений двух групп и определения наличия между ними значимой разницы. Широко применяемый в различных областях, включая биологию, психологию и экономику, t-тест позволяет исследователям анализировать данные и принимать обоснованные решения на основе статистики.

Одной из основных причин широкого применения t-теста Стьюдента является его простота и легкость понимания. В отличие от более сложных статистических тестов, t-тесты легко объяснить и интерпретировать. Это делает их доступными для исследователей с разным уровнем статистических знаний, позволяя им с уверенностью анализировать данные. Кроме того, t-тесты устойчивы к нарушениям некоторых предположений, таких как нормальное распределение и равные вариации, что позволяет использовать их для широкого спектра типов данных и объемов выборок.

Еще одним важным аспектом t-теста является возможность определить, являются ли наблюдаемые различия между двумя группами статистически значимыми: вычисляя t-статистику и сравнивая ее с критическим значением, исследователи могут оценить вероятность того, что эти различия обусловлены случайностью. Если рассчитанное значение t-статистики превышает критическое значение, то это свидетельствует о том, что наблюдаемое различие вряд ли было вызвано только случайной вариацией и является значимым между группами.

Кроме того, t-тест позволяет исследователям делать выводы о популяции на основе выборочных данных: сравнивая средние значения двух групп, можно получить информацию о том, существуют ли реальные различия в средних значениях популяции. Это особенно ценно для исследователей, которые стремятся обобщить свои результаты и сделать выводы для более широкой аудитории.

Обзор t-теста Стьюдента

t-тест Стьюдента - это статистический тест, используемый для определения наличия значимых различий между средними значениями двух групп. Он был разработан Уильямом Госсеттом, который использовал псевдоним "Студент" для работы на пивоваренной компании Guinness. t-тесты основаны на t-распределении - математическом распределении, аналогичном нормальному распределению, но при этом учитываются меньшие размеры выборки. t-тесты используются в психологии, биологии, Этот метод широко используется во многих областях, включая психологию, биологию и экономику.

t-тест используется, когда данные имеют нормальное распределение и дисперсии двух групп приблизительно равны. Он позволяет сравнить средние значения двух независимых групп и определить, является ли наблюдаемое различие между ними статистически значимым. нулевая гипотеза t-теста состоит в том, что различие между средними значениями двух групп отсутствует, альтернативной гипотезой является наличие значимого различия.

Существуют различные типы t-тестов, зависящие от характеристик анализируемых данных. Наиболее распространенными являются независимый выборочный t-тест, в котором сравниваются средние значения двух несвязанных групп, и соответствующий выборочный t-тест, в котором сравниваются средние значения двух связанных групп. Независимый выборочный t-тест используется, когда наблюдаемые значения двух групп независимы друг от друга, а парный выборочный t-тест - когда наблюдаемые значения двух групп зависимы.

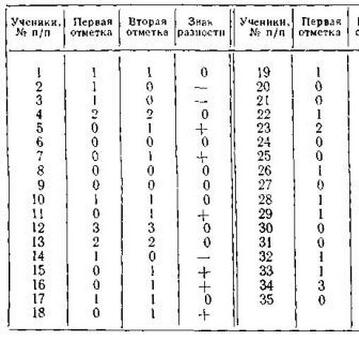
Для проведения t-теста необходимо сначала проанализировать данные двух групп и рассчитать среднее значение, стандартное отклонение и объем выборки. Затем по этим статистическим данным рассчитываются t-значения, которые сравниваются с критическими значениями в таблице t-распределения. Если рассчитанное t-значение больше критического значения, то это свидетельствует о значимой разнице между средними значениями двух групп.

t-тест Стьюдента - это мощный статистический инструмент, позволяющий исследователям анализировать значимость различий между двумя группами. Он дает количественную оценку силы доказательства нулевой гипотезы и помогает исследователям принимать обоснованные решения на основе полученных данных. Однако важно помнить, что t-тест имеет определенные допущения, которые должны быть выполнены, чтобы результаты были достоверными, например, допущения о нормальности и равномерности дисперсии.

Значимость.

Под значимостью понимается важность или релевантность результатов статистического анализа. В контексте t-тестов Стьюдента значимость помогает определить, является ли разница между двумя группами случайной или статистически значимой. Другими словами, она определяет вероятность того, что наблюдаемая разница в средних не является результатом случайной вариации.

Статистическая значимость обычно выражается в виде p-значения и представляет собой вероятность того, что наблюдаемый (или более экстремальный) результат имеет место при нулевой гипотезе. Нулевая гипотеза предполагает отсутствие различий между двумя сравниваемыми группами. Небольшое значение p-value является сильным доказательством против нулевой гипотезы и говорит о том, что наблюдаемые различия вряд ли могут быть обусловлены только случайностью.

Уровень значимости, обозначаемый альфа (α), - это заранее установленный порог, который используется для определения статистической значимости результата. Обычно используются значения альфа 0,05 и 0,01, в зависимости от области исследования и конкретного вопроса. Если p-значение меньше выбранного уровня альфа, то исследователь может отвергнуть нулевую гипотезу и сделать вывод о наличии статистически значимых различий между группами.

Важно отметить, что статистическая значимость не обязательно означает практическую или фактическую значимость. Результат может быть статистически значимым, но не иметь значимого влияния на практике. Поэтому при интерпретации результатов t-теста Стьюдента важно учитывать не только статистическую значимость, но и размер эффекта, доверительные интервалы и практическую значимость.

Значимость t-теста Стьюдента

t-тест Стьюдента - это широко используемый в научных исследованиях и анализе статистический тест. Он позволяет сравнить две группы или выборки и определить, есть ли значимая разница между их средними значениями. Этот тест особенно важен в психологических, биологических и социальных науках, где исследователям часто приходится сравнивать средние значения различных групп.

Одной из основных причин важности t-теста Стьюдента является то, что он позволяет исследователям делать значимые выводы из полученных данных: сравнивая средние значения двух групп, исследователи могут определить, являются ли наблюдаемые различия случайными или статистически значимыми. Это помогает им принимать обоснованные решения и делать точные выводы.

t-тест Стьюдента также важен, поскольку он позволяет количественно оценить неопределенность данных: вычислив t-значение и соответствующее p-значение, исследователи могут определить вероятность того, что наблюдаемые различия обусловлены только случайностью. Это позволяет оценить устойчивость результатов и определить их статистическую значимость.

Кроме того, t-тест Стьюдента широко признан и принят в научном сообществе. Он имеет долгую историю, подробно изучен и валидирован. Исследователи могут быть уверены в результатах, полученных с помощью этого теста, и сравнивать свои результаты с результатами других исследований, в которых использовался тот же метод.

Таким образом, t-тест Стьюдента является важным статистическим инструментом, позволяющим исследователям сравнивать средние значения двух групп и определять наличие значимых различий. Это позволяет делать значимые выводы, количественно оценивать неопределенность и обеспечивать сопоставимость результатов разных исследований. Понимание и правильное использование t-теста Стьюдента необходимо для проведения точных и надежных научных исследований.