Упрощенные формулы умножения
Формулы упрощенного умножения часто используются для умножения многочленов, упрощения формул и упрощения многочленов до стандартной формы. Все доказывается путем раскрытия скобок напрямую и упрощения аналогичных сумм.
Квадратные формулы.
( a + b ) 2 = a 2 + 2 ab + b 2 - сумма квадратов ( a - b ) 2 = a 2 - 2 ab + b 2 - разность квадратов a 2 - b 2 = ( a - b ) ( a + b ) - вторая разность ( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 ab + 2 ac + 2 bc
Математическая формула для куба
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 - куб суммы ( a - b ) 3 = a 3 - 3 a 2 b + 3 a b 2 - b 3 - разность кубов суммы a 3 + b 3 = ( a + b )( a 2 - ab + b 2 ) - куб суммы a 3 - b 3 = ( a - b )( a 2 + ab + b 2 ) - разность кубов суммы
Квадратурная формула
( a + b ) 4 = a 4 + 4 a 3 b + 6 a 2 b 2 + 4 a b 3 + b 4 ( a - b ) 4 = a 4 - 4 a 3 b + 6 a 2 b 2 - 4 a b 3 + b 4 a 4 - b 4 = ( a - b ) ( a + b ) ( a 2 + b 2 )
Формула для n-квадрата
( a + b ) n = a n + na n - 1 b + n ( n - 1) 2 a n - 2 b 2 + . +n! ( n - k ) ! a n - k b k + . + b n (a - b) n = a n - na n - 1 b + n (n - 1) 2 a n - 2 b 2 + . + (-1) k n ! или ! ( n - k ) ! a n - k b k + . + (-1) n b n
Непристойные комментарии будут удалены, а автор занесен в черный список.
Подпишитесь на
Copyright © 2011-2023 Довжик Михаил.
Добро пожаловать в онлайн-школу MS School. Меня зовут Довжик Михаил. Я являюсь владельцем и автором этого сайта. Я написал весь теоретический материал, а также разработал онлайн упражнения и калькуляторы, которые можно использовать для изучения математики.
Если вы хотите связаться со мной, у вас есть вопросы или предложения, или вы хотите помочь в развитии сайта OnlineMSchool, пожалуйста, напишите мне по адресу support@onlinemschool. com A2b2.
Товикинские ресурсы - Томская вики
Пространство имен
Больше.
Мероприятия на этой странице
B2A (произносится как B. to A., bi-to-ay) - это латинский (английский) акроним, обозначающий один из следующих терминов
B2A - Business-to-Administration (дословно: от бизнеса к [регулированию] государственными органами) - это маркетинговый ИТ-термин, обозначающий одну из технологий организаций электронной коммерции. Это одна из тактик электронной коммерции во взаимоотношениях между органами государственной власти (например, государственными учреждениями) и хозяйствующими субъектами (компаниями, предприятиями).
См. также A2B (управление бизнесом), A2C (управление потребителями), B2G (бизнес для правительства), C2A (управление бизнесом/потребителями), G2B (правительство для бизнеса), G2C (правительство для бизнеса) и др.
B2A (XU52C/K) - название одного из типов двигателя автомобилей Peugeot 405 (седан), выпускавшихся с 1987 по 1992 год.
B2A project, арт-центр, - это название казахстанской компании, которая занимается продвижением изобразительного искусства.
YL8 E-B2A - тип топливной форсунки для автомобилей Mazda.
На этой странице объясняется понятие множественных литературных терминов. Нажмите на ссылку с нужным значением.
Что такое B2A?
Что такое B-to-A
Что такое B-to-A
Что такое B-to-A
Все сокращения, пояснения и примеры
Список типов уменьшенного распространения (RMS) в виде таблицы
После обсуждения действий с использованием многочленов и одночленов, в 7 классе алгебры изучаются виды увеличенного умножения. Давайте перечислим их по порядку в списке.
(A+B)2 = A 2+2-A-B+B 2- Так называемый вид квадрата (A-B)2 = A 2-2-A-B+B 2- Этот вид называется квадратом разности (A+B)3 = A 3+3-A 2-B+3-A-B 2+B 3- Этот вид является кубом суммы (A-B)3 = A 3-3-A 2-B+. 3- a-b 2-b 3-Тип куба в споре (a-b) - (a+b) = a 2-b 2 (a-b) - (a 2+a-b+b 2) = a 3- B 3.
Буквы A и B обозначают числа, переменные или, в общем случае, арифметические или буквенные выражения.
Типы сокращенных выражений на самом деле настолько распространены, что целесообразно изучить их все со стороны. До тех пор рекомендуется распечатать и иметь всегда перед собой верный экземпляр.
Первые четыре типа панели сокращенного умножения можно использовать для возведения в квадрат суммы или разности двух выражений; пятый тип используется для сокращенного умножения разности и суммы двух выражений; шестой и седьмой типы используются для умножения суммы двух выражений a и b на неполный квадрат их разности (выражение 2-a -b+b 2 ) и разности двух выражений a и b используется для умножения разницы между a и b. неполный квадрат каждого из них (a 2 + a-b +b 2).
Стоит отдельно отметить, что каждое равенство в таблице является тождеством. Это объясняет, почему вид уменьшаемого при умножении также называют тождеством уменьшаемого при умножении.
При решении примеров, особенно тех, которые связаны с разложением многочленов на множители, ФСУ часто используется в перестановочной форме левой и правой части.
Последние три идентификатора в таблице имеют собственные имена. Формула a 2-b 2 =(a-b)-(a+b) называется формулой квадрата разности, а a 3 +b 3 =(a+b)-(a 2-a-b+b 2 ) - формулой квадрата разности. Формула для суммы кубов, a 3-b 3 =(a-b)-(a 2 +a-b+b 2 ), называется формулой куба разности. Обратите внимание, что мы не назвали соответствующие типы, которые переставляют части предыдущей таблицы.
Вывод формулы разности кубов
Чтобы доказать справедливость формулы разности кубов, достаточно раскрыть скобки и умножить формулу
( a - b ) - ( a 2 + ab + b 2 ) = = a 3 + a 2 b + a b 2 - b a 2 - a b 2 - b 3 = a 3 - b 3
Основные задачи для формул упрощенного умножения
Внимание!
Если вам нужна помощь с академической статьей, мы рекомендуем вам обратиться к эксперту - более 70 000 экспертов готовы помочь вам прямо сейчас.
Формулы расширенного умножения (Eqs) используются для умножения и повышения силы чисел, выражений, включая многочлены. Это означает, что с помощью формул вы можете работать с числами быстрее и проще. Таким образом, сложные уравнения могут быть превращены в простые уравнения, что упрощает вашу работу.
Сумма квадратов двух уравнений
В некоторых случаях умножение многочленов и полиномов может быть значительно упрощено. Так, например, в случае (2 x + 3 y ) 2
Выражение (2 x + 3 y ) 2 является умножением двух многочленов, каждый из которых равен (2 x + 3 y ).
Мы получили умножение многочлена на многочлен. Выполнить: .
То есть, выражение (2 x + 3 y ) 2 равно 4 x 2 + 12 xy + 9 y 2 .
Решим более простой аналогичный пример.
Выражение ( a + b ) 2 является произведением двух многочленов, каждый из которых равен ( a + b ).
Выполним это умножение.
То есть, выражение ( a + b ) 2 равно a 2 + 2 ab + b 2
Видно, что случай (a + b) 2 может быть расширен для любых a и b. Первый решенный пример, то есть (2 x + 3 y ) 2 , можно решить с помощью тождества (a + b ) 2 = a 2 + 2 ab + b 2 . Для этого соответствующие члены в уравнении (2 x + 3 y ) 2 заменяются переменными a и b. где переменная a - член 2 x, а переменная b - член 3 y.
Затем можно использовать единицы ( a + b ) 2 = a 2 + 2 ab + b 2, но вместо переменных a и b подставить выражения 2 x и 3 y соответственно.
Как и раньше, существует многочлен 4 x 2 + 12 xy + 9 y 2 . Решения обычно пишутся в коротких предложениях путем мысленного выполнения всех основных изменений.
Тождество (A + B)2 = A 2 + 2 AB + B 2 называется квадратным видом двух уравнений. Этот тип может быть прочитан следующим образом:.
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе выражение.
Рассмотрим уравнение (2 + 3)2 , которое можно вычислить двумя способами: добавив скобку к первому уравнению и добавив квадрат ко второму уравнению. Либо добавьте скобки для возведения в квадрат, либо используйте тип для возведения в квадрат суммы двух выражений.
Первый метод.
(2 + 3)2 = 5 2 = 25
Второй метод:.
(2 + 3)2 = 2 2 + 2 x 2 x 3 + 3 2 = 4 + 12 + 9 = 25
Пример 2. Превратите выражение (5 A + 3)2 в многочлен.
Используйте квадратный вид суммы двух выражений.
(5 A + 3)2 = (5 A)2 + 2 x 5 A x 3 + 3 2 = 25 A 2 + 30 A + 9
Решите этот пример без использования типа квадратной суммы. Нам нужен тот же результат.
Тип квадрата суммы - геометрический. Помните, что для вычисления площади квадрата необходимо увеличить его сторону до второй степени.
Например, площадь квадрата со стороной A равна 2. Если сторону квадрата увеличить на B, то площадь будет равна (a + b)2
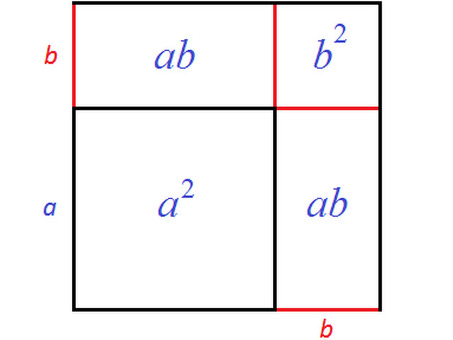
Рассмотрим следующий рисунок: .
Представьте, что сторона квадрата, изображенного на этом рисунке, увеличилась на b. Все стороны квадрата равны. Если его сторона увеличивается на b, то другая сторона также увеличивается на b
Возьмите новый квадрат, который больше предыдущего. Чтобы увидеть это наглядно, добавьте недостающую сторону.
Чтобы вычислить площадь этого квадрата, можно вычислить составляющие его квадраты и прямоугольники по отдельности и сложить результат.
Во-первых, можно вычислить квадрат со стороной A - его площадь равна 2. Далее можно вычислить прямоугольник со сторонами a и b - его площадь равна AB. Тогда вы можете вычислить квадрат со стороной b
Результатом является сумма поверхностей следующим образом
Сумму площадей одинаковых прямоугольников можно заменить умножением на 2 AB. Это буквально означает "повторение удвоенной площади прямоугольника AB". Алгебраически это приводит к сложению одинаковых сумм ab и ab. В результате получается 2 + 2 Ab + B 2. Это правильная часть двух видов выражения суммы.
Квадрат разницы между двумя выражениями
Формула для квадрата разности двух выражений имеет вид
Эта формула может быть прочитана следующим образом.
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
Выражение для квадрата разности двух выражений выводится так же, как и выражение для квадрата суммы двух выражений. ( a - b ) 2 - это произведение двух многочленов, каждый из которых равен ( a - b ).
Выполнение этого умножения дает многочлен a 2 - 2 ab + b 2.
Пример 1. Преобразуйте выражение (7 x - 5) 2 в многочлен.
Используйте формулу для квадрата разности двух выражений.
(7 x - 5) 2 = (7 x ) 2 - 2 × 7 x × 5 + 5 2 = 49 x 2 - 70 x + 25
Решите этот пример без использования формулы квадратичной разности. Вы должны получить тот же результат.
Формула квадрата разности двух выражений также имеет геометрический смысл. Если площадь квадрата со стороной a равна a 2, то площадь квадрата, стороны которого уменьшены на b, равна (a - b) 2.
Рассмотрим следующий рисунок: .
Предположим, что одна сторона квадрата, изображенного на этой диаграмме, уменьшается на b. Все стороны квадрата равны. Если одна сторона уменьшается на b, то другая сторона также уменьшается на b
Вы получаете новый квадрат, который меньше предыдущего. Он показан желтым цветом. Старая сторона a короче на b, поэтому эта сторона равна a - b. Чтобы вычислить площадь этого квадрата, из площади исходного квадрата можно вычесть площадь прямоугольника, полученного при уменьшении сторон старого квадрата. Покажите эти прямоугольники:
Затем мы можем написать следующее уравнение: старая площадь a 2 минус площадь ab площадь (a - b ) b
Открываем скобки в выражении ( a - b ) b
Добавим аналогичную сумму.
В результате получается выражение a 2 - 2 ab + b 2. Это правая часть выражения для квадрата разности между двумя выражениями.
Формулы для квадрата суммы и квадрата разности принято называть упрощенным умножением. Эти формулы значительно упрощают и ускоряют умножение многочленов.
Ранее мы говорили, что при рассмотрении членов многочлена по отдельности, знак, предшествующий им, также должен рассматриваться вместе.
Однако при применении упрощенных формул умножения знак исходного многочлена не следует рассматривать как знак самого члена.
Например, учитывая выражение (5 x-2 y)2 и используя вид ( a-b)2 = a 2-2 ab + b 2, используйте 2 y вмест о-2 для b. y. Это специфика типа, о которой нельзя забывать.
-2 y вместо y. Это означает, что разность между скобками в исходном уравнении заменяется суммой.
Поэтому не следует использовать квадратичный тип спора, а использовать тип суммы: -2 y - 2 y.
Исключением является выражение вида (x - (- y))2 . В этом случае вместо вида (a - b) 2 = b ( - y) следует использовать 2-2 ab + b 2.
Однако если выражение вида x - (- y) является квадратным, то удобнее заменить удаление сложением x + y. Тогда исходное уравнение имеет вид (x + y)2, а вместо разности можно использовать сумму квадратов.
Квадратурная формула
( a + b ) 4 = a 4 + 4 a 3 b + 6 a 2 b 2 + 4 a b 3 + b 4 ( a - b ) 4 = a 4 - 4 a 3 b + 6 a 2 b 2 - 4 a b 3 + b 4 a 4 - b 4 = ( a - b ) ( a + b ) ( a 2 + b 2 )
Как читается тип увеличения умножения?
Чтобы понять решение примера, где используются типы убывающего умножения, нужно знать, как читать эти типы. Приведем соответствующие типы.
Во-первых, поймите принцип чтения сокращенных видов умножения. Лучше всего это сделать, например, взяв один из них. Например, первый тип совокупности (a+b)2 = a 2+2-a-b+b 2.
В левой части стоит (A+B)2 . Это читается как квадрат суммы двух выражений A и B (отсюда и название). Далее следует символ равенства. Это выражается в равенстве. Правая часть вида содержит сумму трех членов A 2, 2-A-B и B 2. A2 и B 2 - квадраты первого и второго членов соответственно, а 2-A-B читается как двойное произведение A b, где слово "двойной" соответствует числовому коэффициенту 2. Именно сочетание всех этих умозаключений в одном предложении отвечает на вопрос о том, как читается тип для подведения итогов.
Таким образом, квадрат суммы двух выражений a и b равен сумме квадратов первого выражения, дубликатов первого и второго выражений и квадрата второго выражения.
Другие ФГУ считываются аналогичным образом.
Таким образом, квадрат разности двух выражений равен квадрату первого выражения минус квадрат этих выражений умноженный на два и квадрату второго выражения; это утверждение во втором ФСУ имеет вид (A-B)2 = A 2-2-A-B+B 2.
Затем читаем выражение (a+b) 3 =a 3 +3-a 2-b+3-a-b 2 +b 3. Куб суммы двух выражений a и b равен сумме кубов первого выражения, тройного произведения квадрата первого выражения, умноженного на квадрат второго выражения, и произведения куба первого выражения, умноженного на квадрат второго выражения. второе уравнение, и куб второго уравнения.
Куб разности (α-β) 3 =α 3-3-α 2-β+3-α-β 2-β 3 аналогично: куб разности двух выражений равен сумме куба первого выражения минус кубическое произведение квадрата первого выражения, умноженного на квадрат второго выражения, и кубического произведения первого выражения, умноженного на квадрат второго выражения минус квадрат равны. Второе выражение.
Продолжите чтение пятого выражения в списке сокращений (a-b)-(a+b)=a 2-b 2. Произведение разности двух выражений и их суммы равно разности между первым выражением и квадратом второго выражения.
Затем, чтобы облегчить чтение шестого и, наконец, седьмого FSE, используя термины "неполный квадрат суммы" и "неполный квадрат разности" выражений a и b, выражения a 2 +a-b+b 2 и a 2-a-b+b 2 ...).
Таким образом, произведение суммы двух выражений, умноженное на неполный квадрат их разности, равно сумме кубов этих выражений. Таким образом, уравнение имеет вид (a+b)-(a 2-a-b+b 2 ) = a 3 +b 3 . Тогда произведение разности двух выражений и неполного квадрата их суммы равно разности. Из кубов этих выражений этому утверждению соответствует выражение сокращенного умножения вида (α-β)-(α 2 +α-β + β 2 )=α 3-β 3.
Возведение сумм в квадрат
Формула для квадрата суммы представляет собой равенство
(квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа, умноженного на второе число, плюс квадрат второго числа).
В этой формуле a и b можно заменить любым числом.
Формула для суммы квадратов часто используется для упрощения вычислений. Например.
Формула суммы квадратов может быть использована для определения коэффициентов многочленов. То есть, его можно выразить как произведение двух одинаковых факторов. Например, формула суммы квадратов может быть использована для факторизации полиномиального выражения, то есть оно может быть выражено как произведение двух одинаковых факторов.
Выражение следует правилам умножения многочленов.
Пример 1: Запись выражения
Решение. Используя формулу для суммы квадратов, мы имеем
Пример 2: Запись выражения
Решение. Используя формулу для суммы квадратов, мы имеем
Вам нужно самостоятельно применить формулу сжатия, прежде чем вы сможете найти решение.
Пример 3. Выяснить, является ли многочлен
является многочленом в квадрате.
Правильное решение и ответ.
Пример 4. Отказ от умножения
Правильное решение и ответ.
Экспорт общих квадратов
Часто полином второй степени содержит полный или разностный квадрат, но в скрытой форме. Чтобы получить полный квадрат в явном виде, многочлен необходимо преобразовать. Для этого одно из условий многочлена обычно выражается в виде двойного произведения, и одно и то же число добавляется к многочлену и удаляется из него.
Пример 7. Рассмотрим многочлен второй силы
Решение. Этот полином может быть преобразован следующим образом.
где 5 x выражается как двойное произведение 5/2 на x. Прибавить к многочлену и отнять то же число. Затем этот тип был применен к суммарным биохимическим показателям. Мы применили этот тип к сводным итоговым показателям BIM.
Таким образом, мы доказали равенство.
Это показывает, что второй является многочленом мощности
равна общей площади плюс число и число.
Пример 8. Рассмотрим многочлен второй степени
Решение. Выполните следующее преобразование.
Здесь мы воспроизвели 8 x как двойное произведение x на 4. К многочлену прибавлено и от него отнято одно и то же число 4². Мы применили этот тип к квадрату разности границ x - 4.
Таким образом, мы доказали равенство.
Это показывает, что второй является многочленом мощности
равна общему квадрату плюс числ о-16.
Вам нужно самостоятельно применить формулу сжатия, прежде чем вы сможете найти решение.
Пример 9. Определение полного квадрата с помощью полинома второй мощности
Правильное решение и ответ.
Дополнительные типы.
Добавление некоторых дополнительных тождеств к сокращенной таблице мультипликативных типов - неплохая идея.
Во-первых, можно использовать форму биномиального типа Ньютона. Здесь биномиальные коэффициенты находятся в n-м числе треугольников Паскаля; для их сокращения до физической степени можно использовать сумму двух выражений. Кстати, квадратичное ФСУ и сумма и разность суммы являются частными случаями биномиального типа Ньютона для n = 2 и n = 3.
Она гласит: квадрат из n слагаемых равен сумме квадратов всех этих слагаемых и дубликату всех возможных пар этих слагаемых. Используйте этот тип для получения суммы трех слагаемых a, b и c. Это дает (a + b + c)2 = a 2 + b 2 + c 2 + 2-a-b + 2-a-c + 2-b-c. В частном случае n = 2 этот вид является известным видом квадрата двух сумм.
Это также помогает иметь вид разности между двумя n-силами вида A n-b n = = (a-b) - (a n-1 +a n- 2-b +a n- 3-b, всего два. 2 +... +a-b n-2 +b n-1). Обычно это представляется отдельно для весов и ненужных чисел. Для масштаба 2-m получается вид 2- m-b 2-m = = (a 2-b 2) - (a 2-m-2 +a 2-m- 4-b 2 +a 2-m- (a 2-m-2 +a 2-m-)). 6-b 4+... +b 2-m-2), а для ненужного числа 2-m+1, 2-m+ 1-b 2-m+1 = = (a-b) - ( 2-M +A 2-M- 1-B +A 2-M- 2-B 2 +... +B 2-M). Особыми случаями этого типа являются типы квадратной разности (для n = 2), кубов разности (для n = 3) и кубов суммы (для n = 3 и b заменено н а-b).
Кубики суммы и разности.
Тип куба для суммы двух выражений и куба разности двух выражений следующие
Вид куба суммы двух выражений может быть прочитан следующим образом
Куб суммы двух выражений равен кубу первого выражения плюс тройное произведение квадрата первого выражения на квадрат второго выражения, равный тройному произведению квадрата первого выражения на квадрат второго выражения, равный кубу второго выражения. .
Тогда человек кубов этих двух выражений может быть прочитан следующим образом
Куб разности двух выражений равен кубу первого выражения, плюс тройное произведение квадрата первого выражения на второе выражение, минус тройное произведение квадрата первого выражения на второе выражение, минус куб второго выражения.
При решении проблемы желательно знать эти типы извне. Если вы их не помните, не беда! Вы можете найти их сами. Мы уже знаем, как это сделать.
Давайте экспортируем тип общей суммы.
Выражение (a + b)3 является произведением трех многочленов, каждый из которых равен (a + b)
Однако (a + b)3 также можно записать как (a + b)(a + b)(a + b)2 .
Коэффициент (a + b)2 - это квадрат суммы двух выражений. Эта сумма квадратов равна выражению a 2 + 2 ab + b 2.
Это умножение многочлена на многочлен. Давайте попробуем:.
Кубические типы различий между двумя выражениями могут возникать одинаково.
Пример 1. Превратите выражение (x + 1)3 в многочлен.
Используйте тип для суммирования двух экспресс-сумм.
(x + 1)3 = x 3 + 3 x x 2 x 1 + 3 x x 1 2 + 1 3 = x 3 + 3 x 2 + 3 x 2 + 3 x + 1
Попробуем решить этот пример без использования двух типов кубов выражений. Эффект тот же, но решение более масштабное.
Пример 2. Преобразуйте выражение (6 A 2 + 3 B 3)3 в многочлен.
Используйте тип для суммирования двух экспресс-сумм.
(6 A 2 + 3 B 3)3 = (6 A 2)3 + 3 x (6 A 2)2 x 3 B 3 + 3 x 6 A 2 x (3B 3)2 + (3 B 3)3 = 216 A 6 + 3 x 36 A 4 x 3 B 3 + 3 x 6 A 2 x 9 B 6 + 27 B 9
Пример 3. Превратите уравнение (n 2-3)3 в многочлен.
Используйте тип для кубика разницы между двумя выражениями.
(n 2-3)3 = (n 2)3-3 x (n 2)2 x 3 + 3 x n 2 x 3 2-3 3 = n 6-9 n 4 + 27 n 2-27
Пример 4. Преобразовать уравнение (2 x 2-x 3)3 в многочлен.
Используйте тип для кубика разницы между двумя выражениями.
Пример задачи с использованием типа куба разностей.
Разделите x 3-27 более чем на один.
x 3-27 = x 3-3 3 = ( x-3) - (x 2 + 3 x + 9)
Снимите x 3-27 y 6 с агента 8 x 3-27 y 6.
8 x 3-27 y 6 = (2 x) 3 - (3 y 2) 3 = (2 x-3 y 2) - (4 x 2 + 6 xy 2 + 9 y 4)
Упростите уравнение 27 x 3-1 3 x-1.
Разность кубов может показаться применимой к уравнению с числителем
27 x 3-1 3 x-1 = (3 x-1) - (9 x 2 + 3 x +1) 3 x-1 = 9 x 2 + 3 x +1
Как вычислить разницу между кубами
Рассмотрим пример. Вам нужно сгенерировать разницу между кубами.
Обратите внимание, что "27a 3" - это "(3a)3". Поэтому вместо 'a' используйте '3a' для типа разности кубов.
Используйте тип для различия кубов. Вместо "a 3" стоит "27a 3" и, как в СМИ, "b 3" в позиции "b 3".
Площадь.
Это квадрат разности, также называемый совершенным квадратом разности в выражении.
Он называется неполным квадратом разности; неполный квадрат разности двух чисел равен квадрату первого числа, который равен произведению первого числа на второе число и квадрату второго числа. Неполный квадрат разности отличается от полного только в том случае, если количество чисел не удваивается.
Группа типов: сумма сил
Группы типов, суммы баллов, представлены в таблице 2. Эти типы могут возникнуть в результате выполнения вычислений в следующем порядке.
(x + y)2 = (x + y) (x + y), (x + y)3 = (x + y)2 (x + y), (x + y)4 = (x + y)3 (x + y)
Тип группы "сумма сил" может возникнуть при использовании треугольника Паскаля и бионима Ньютона.
Таблица 2.- Сумма сил
сумма (x + y)2 = x 2 + 2 xy + y 2 Куб (третья степень) сумма (x + y)2 = x 2 + 2 xy + y 2 Куб (x + y)3 = x 3 + 3 x 2 y + 3 x y 2 + y 3 Четверть (x + y)4 = x 4 + 4 x 3 y + 6 x 2 y + 4 x 2 y 3 + y сумма пятый класс (x + y)5 = x 5 + 5 x 4 + 10 x 3 y (2 y) 4 = x 4 + 4 x 3 y + 6 x 2 y 2 + 4 x y 3 + y сумма (x + y) 5 = x 5 + 5-я сила 5 x 4 y + 10 x 3 y 2 + 10 x 2 y 3 + 5 x y 4 + y 5 сумма (x + y) 6 = x 6 + 6 x 5 y + 15 x 4 y 2 + 20 x 3 y 3 + 15 x 2 y 4 + 6 x y 5 + y 6
Общий тип для вычисления суммы
с использованием произвольного натурального значения n описано в разделе руководства "Биномиальный бином Ньютона".
Различия в мощности
Замена y на y типа, приведенного в таблице 2, дает "группу различий" (таблица 3):.
Таблица 3 - Различия в мощности.
Название Тип Название Тип Название Квадрат ( x-y)2 = x 2-2 xy + y 2 Куб (3-я степень) Разность ( x-y)3 = x 3-3 x 2 y + 3 x y 2-y 3 Разность Четверть ( x-y)4 = x 4-4 x 3 y + 6 x 2 y 2-4 x y 3 + y 4 5-я степень Разность ( x-y)5 = x 5-5 x 4 y + 10 x 3 y 2-10 x 2 y 3 + 5 x y 4 -... y 5 6 Разность степеней ( x-y) 6 = x 6-6 x 5 y + 15 x 4 y 2-20 x 3 y 3 + 15 x 2 y 4-6 x y 5 + y 6
http://www. cleverstudents. ru/expressions/formulas_of_short_multiplication. html
https://ru. onlinemschool. com/math/library/multiplication_formulas/dif33/
https://nauchniestati. ru/spravka/formuly-sokrashhjonnogo-umnozhenija/
http://spacemath. xyz/formuly-sokrashhennogo-umnozheniya/
https://ru. onlinemschool. com/math/formula/multiplication_formula/
https://function-x. ru/formuly_sokrashchennogo_umnozhenija. html
http://math-prosto. ru/? page=pages/how_use_use_formulas_of_abridged_multiplication/difference_of_cubes. php
https://nobumium. info/algebra/formuly_sokr_umnojeniya. php
http://www. studik. keiv. ua/ru/formuly-sokrashhennogo-umnozhenija/
Что касается нас.
'A2 Group' осуществляет комплексную поставку электротехнических изделий для строительно-монтажных организаций, промышленных предприятий, магазинов и коммерческих компаний. Благодаря нашему многолетнему опыту и комплексному подходу, любые поставленные вами задачи мы решаем в кратчайшие сроки.
Наши преимущества
Широкий ассортимент продукции
Мгновенная доставка
Работники-специалисты
Гибкое ценообразование
A2 Group - продажа электротехники
Широкий ассортимент продукции позволяет нам на 100% удовлетворять потребности наших клиентов.
Комплексная поставка следующих продуктов
Проводка и электропроводка
Освещение
Электричество
Молния - Защитные устройства
Системы безопасности
Расположение панелей
Разложение многочленов с типами редукции
Пример 4*. Выразите сумму или разность в виде куба.
(a) $ 8m^3 k^3+12m^2 k^2+6mk+1 = (2mk)^3+3 \ cdot(2mk)^2 \ cdot1+3 \ cdot2mk \ cdot1^2+1^3 = $
(b)$ 125b^3-225b^2 c+135bc^2-27c^3 = (5b)^3-3 \ cdot(5b)^2 \ cdot3c+3 \ cdot5b \ cdot(3c)^2-(3c(3c))^3 = $
Пример 5. Отправка на множители:.
(a)$ 25a^2-b^2+5a+b = (25a^2-b^2)+(5a+b) = (5a+b) (5a-b)+(5a+b) = $
(b)$ x-2y-x^2+4y^2 = (x-2y) - (x^2-4y^2) = (x-2y) - (x-2y) (x+2y) = $
Пример 6. Отправка на множители:.
(a) $ xz^2+yz-yz^2-xz = z(xz+yz-x) = z((xz-yz) - (x-y)) = $
(b) xz+yz-2z-ax z-yz+2az = z(x+y-2-a x-y+2a) = $
Пример 7*. Свернуть в множитель:.
(a) $ a^4+64 = (a^4+16a^2+64)-16a^2 = (a^2+8)^2-(4a)^2 = $
(b)$ x^4+324 = (x^4+36x^2+324) - 36x^2 = (x^2+18) - (6x)^2 = $
(c)$ a^4+4b^4 = (a^4+4a^2 b^2+4b^4)-4a^2 b^2 = (a^2+2b^2)^2-(2ab)^2 = $
Пример 8. Решение уравнения Декарта (1596-1650)
$ (y^2-1) (y-8) = 0 \ rightArrow (y+1) (y-1) (y-8) = 0 \ rightarrow \ left [\ begin y_1 = -1 \ y_2 = 1 \ y_3 = 8 \ end \ right. $
Ответ: $ \ pm $ 1; 8
Пример 9*. решить уравнение Бхаскары (1114-1185).
Вторая скобка всегда положительна и не может быть равна нулю. Первая скобка выглядит следующим образом.
$$(x-1)^2-10^2 = 0 \ rightArrow (x-1-10) (x-1+10) = 0 \ rightArrow \ left [\ begin x_1 = 11 \ x_2 = -9 \ end \ right. $$





Комментарии